回溯算法的基本思想：实际上是一个类似枚举的搜索尝试过程，主要是在搜索尝试过程中寻找问题的解，当发现不满足求解条件时，就“回溯”返回，尝试别的路径。是一种选优搜索法，按选优条件向前搜索，以达到目标。

回溯算法经常以递归的方式实现，用来解决以下3类问题：

  • 决策问题：从众多选择中找到一个可行的解决方案；
  • 优化问题：从众多选择中找到一个最佳的解决方案；
  • 枚举问题：找出解决问题的所有方案。

经典问题有：N皇后问题，迷宫问题等。

找到从A到K的行走路线

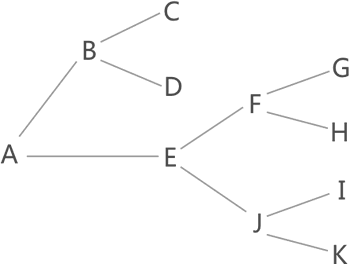
回溯算法—找从A-K的行走路线

解题思路：

所谓“回溯”，其实就是回退、倒退的意思。仍以图 1 为例，回溯算法查找从 A 到 K 路线的过程是：

  • 从 A 出发，先选择 A-B 路线；继续从 B 出发，先选择 B-C 路线；到达 C 点后发现无路可选，表明当前路线无法达到 K 点，该算法会立刻回退到上一个节点，也就是 B 点；
  • 从 B 点出发，选择 B-D 路线，达到 D 点后发现无法到达 K 点，该算法再回退到 B 点；
  • 从 B 点出发已经没有新的线路可以选择，该算法再次回退到 A 点，选择新的 A-E 路线；
  • 继续以同样的方式测试 A-E-F-G、A-E-F-H、A-E-J-I 这 3 条线路后，最终找到 A-E-J-K 路线。

回溯算法的经典应用

迷宫问题

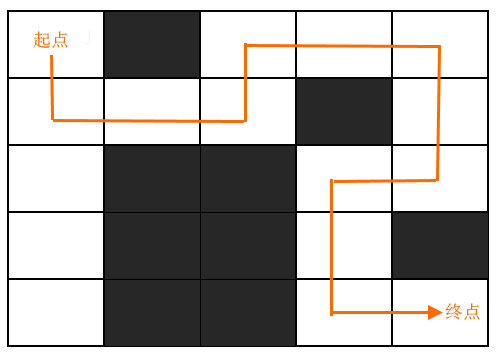
迷宫问题是指：在给定区域内，找到一条甚至所有从某个位置到另一个位置的移动路线。如下图：在白色区域内找到一条（甚至所有）从起点到终点的路线。

解决思路：

  1. 从当前位置开始，分别判断是否可以向 4 个方向（上、下、左、右）移动：
  2. 选择一个方向并移动到下个位置。判断此位置是否为终点，如果是就表示找到了一条移动路线；如果不是，在当前位置继续判断是否可以向 4 个方向移动；
  3. 如果 4 个方向都无法移动，则回退至之前的位置，继续判断其它的方向；
  4. 重复 2、3 步，最终要么成功找到可行的路线，要么回退至起点位置，表明所有的路线都已经判断完毕。

迷宫问题

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
// 用 1 表示白色区域，用 0 表示黑色区域。
internal class Program
{
    private static int ROW = 5;
    private static int COL = 5;

    private static bool find = false;

    private static void Main(string[] args)
    {
        char[,] maze = new char[,]
        {
            {'1','0','1','1','1'},
            {'1','1','1','0','1'},
            {'1','0','0','1','1'},
            {'1','0','0','1','0'},
            {'1','0','0','1','1'}
        };
        maze_puzzle(maze, 0, 0, ROW - 1, COL - 1);
        if (!find)
        {
            Console.WriteLine("该迷宫无解");
        }
    }

    // 起点：(row, col)     终点：(outRow, outCol)
    private static void maze_puzzle(char[,] maze, int row, int col, int outRow, int outCol)
    {
        maze[row, col] = 'Y'; // 将走过的区域标记为 Y
        // 如果走到终点，则表明起点到终点有路线
        if (row == outRow && col == outCol)
        {
            find = true;
            Console.WriteLine("成功走出迷宫，路线图是：");
            printMaze(maze);
            return;
        }
        // 判断上方是否可移动
        if (canMove(maze, row - 1, col))
        {
            maze_puzzle(maze, row - 1, col, outRow, outCol);
            // 如果程序不结束，则此路不通，恢复该区域的标志
            maze[row - 1, col] = '1';
        }
        // 判断左方是否可移动
        if (canMove(maze, row, col - 1))
        {
            maze_puzzle(maze, row, col - 1, outRow, outCol);
            // 如果程序不结束，则此路不通，恢复该区域的标志
            maze[row, col - 1] = '1';
        }
        // 判断下方是否可移动
        if (canMove(maze, row + 1, col))
        {
            maze_puzzle(maze, row + 1, col, outRow, outCol);
            // 如果程序不结束，则此路不通，恢复该区域的标志
            maze[row + 1, col] = '1';
        }
        // 判断右方是否可移动
        if (canMove(maze, row, col + 1))
        {
            maze_puzzle(maze, row, col + 1, outRow, outCol);
            // 如果程序不结束，则此路不通，恢复该区域的标志
            maze[row, col + 1] = '1';
        }
    }

    private static bool canMove(char[,] maze, int row, int col)
    {
        // 判断输入的位置是否在迷宫范围内，且可移动，且还未移动过
        return row >= 0 && row <= ROW - 1 && col >= 0 && col <= COL - 1
            && maze[row, col] != '0' && maze[row, col] != 'Y';
    }

    private static void printMaze(char[,] maze)
    {
        for (int i = 0; i < ROW; i++)
        {
            for (int j = 0; j < COL; j++)
            {
                Console.Write(maze[i, j] + " ");
            }
            Console.WriteLine();
        }
    }
}

输出：

成功走出迷宫，路线图是：
Y 0 Y Y Y
Y Y Y 0 Y
1 0 0 Y Y
1 0 0 Y 0
1 0 0 Y Y

N皇后问题

N皇后问题源自国际象棋，所有棋子中权力最大的称为皇后，它可以直着走、横着走、斜着走（沿45度角），可以攻击移动途中遇到的任何棋子。N皇后问题的具体内容是：如何将N个皇后摆放在N*N的棋盘中，使它们无法相互攻击。如下图所示。

解决思路：

要想使 N 个皇后不相互攻击，应将它们放置在不同的行、不同的列、还不能位于同一条 45°（或 135°）角的斜线上。

回溯算法解决N皇后问题的具体思路是：将 N 个皇后逐一放置在不同的行，以“回溯”的方式逐一测试出每行皇后所在行的具体位置，最终确定所有皇后的位置。

N皇后问题

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
internal class Program
{
    private static int[] q = new int[20]; // 每个皇后的所在列数
    private static int count = 0; // count 种解决方案

    private static void Main(string[] args)
    {
        Console.Write("请输入皇后的个数：");
        string sc = Console.ReadLine();
        int n = int.Parse(sc);
        n_queues(1, n);
        Console.WriteLine("共有 " + count + " 种摆放方式");
    }

    /// <summary>
    /// N皇后算法
    /// </summary>
    /// <param name="k">第几行数</param>
    /// <param name="n">皇后个数</param>
    private static void n_queues(int k, int n)
    {
        int j;
        // 递归出口：当前行数大于皇后个数
        if (k > n)
        {
            print(n);
        }
        else
        {
            // 尝试第 k 行的每一列，找到符合要求的列
            for (j = 1; j <= n; j++)
            {
                if (isSafe(k, j))
                {
                    // 存进数组中保存
                    q[k] = j;
                    // 确认第 k 行皇后位置后，继续下一行的皇后的位置判断。
                    n_queues(k + 1, n);
                }
            }
        }
    }

    private static bool isSafe(int k, int j)
    {
        int i;
        // 判断是否有其他皇后位置在同一列，或者位于该位置的斜线位置上，如果有，则不能放
        for (i = 1; i < k; i++)
        {
            // 同一斜线判断规则：|行号差值| = |列号差值|
            if (q[i] == j || Math.Abs(i - k) == Math.Abs(q[i] - j))
            {
                return false;
            }
        }
        return true;
    }

    private static void print(int n)
    {
        int i, j;
        count++;
        Console.WriteLine("第 " + count + " 个解为：");
        for (i = 1; i <= n; i++) // 行
        {
            for (j = 0; j <= n; j++) // 列
            {
                if (q[i] != j)
                {
                    Console.Write("x");
                }
                else
                {
                    Console.Write("Q");
                }
            }
            Console.WriteLine();
        }
        Console.WriteLine();
    }
}

输入：4

第 1 个解为：
xxQxx
xxxxQ
xQxxx
xxxQx

第 2 个解为：
xxxQx
xQxxx
xxxxQ
xxQxx

共有 2 种摆放方式