算法——动态规划算法
动规的基本思想:动规的实质是分治思想和解决冗余。将原问题分解为若干子问题,通过解决子问题的最优解来得到原问题的最优解。是一种解决多阶段决策问题的优化方法。
与分治算法的不同之处在于,分治算法拆分出的小问题之间是相互独立的,而动规拆分的小问题之间是相互关联的,想要解决问题 A ,就必须先解决问题 B 和 C。
动态规划算法的关键在于将原问题分解为子问题,并利用子问题的最优解来构造原问题的最优解。通过状态转移方程的定义和递推求解过程,动态规划算法能够避免重复计算,提高问题求解的效率。它适用于那些具有重叠子问题和最优子结构性质的问题,如最短路径问题、背包问题、序列比对等。(空间换时间的算法)
动规算法的解题思路
用 f(n) 表示凑齐面值 n 所需纸币的最少数量,面值 15 的拼凑方案有 3 种,分别是:
- f(15) = f(14) +1:挑选一张面值为 1 的纸币,f(14) 表示拼凑出面值 14 所需要的最少的纸币数量;
- f(15) = f(8) + 1:挑选一张面值为 7 的纸币,f(8) 表示拼凑出面值 8 所需要的最少的纸币数量;
- f(15) = f(5) + 1:选择一张面值为10 的纸币,f(5) 表示拼凑出面值 5 所需要的最少的纸币数量。
也就是说,f(14)+1、f(8)+1 和 f(5)+1 三者中的最小值就是最优的拼凑方案。采用同样的方法,继续求 f(14)、f(8)、f(5) 的值:
- f(5) = f(4) + 1;
- f(8) = f(7) + 1 = f(1) +1;
- f(14) = f(13)+1 = f(7) + 1 = f(4) +1。
动态规划算法的经典应用
0-1背包问题
虚拟一个场景,商店中拥有 5 件商品,它们各自的重量和收益分别是:
- 商品 1:重量 1 斤,收益 1 元;
- 商品 2:重量 2 斤,收益 6 元;
- 商品 3:重量 5 斤,收益 18 元;
- 商品 4:重量 6 斤,收益 22 元;
- 商品 5:重量 7 斤,收益 28 元。
所有商品不可再分,顾客要么“整件”购买商品,要么放弃购买。一个小偷想窃取商品,他的背包只能装 11 斤商品,如何选择商品才能获得最大的收益呢?
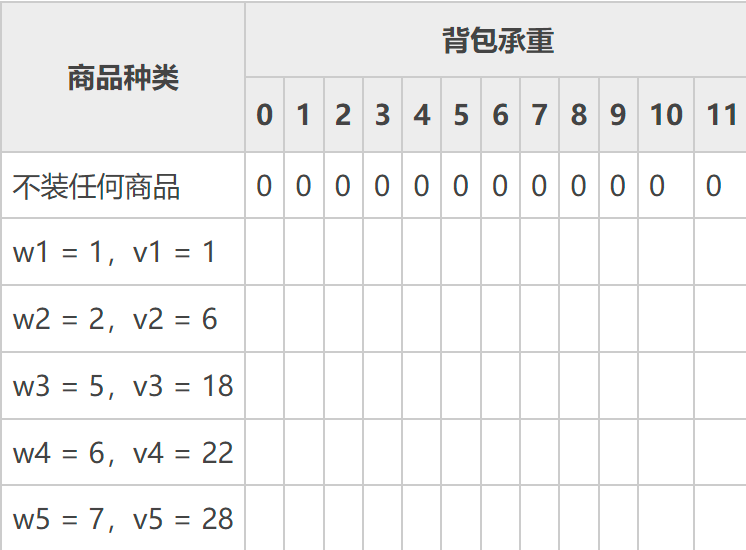
表格中,wi 表示第 i 件商品的重量,vi 表示第 i 件商品的收益值。承重不同的各个背包尚未装入商品时,对应的收益值都为 0。
-
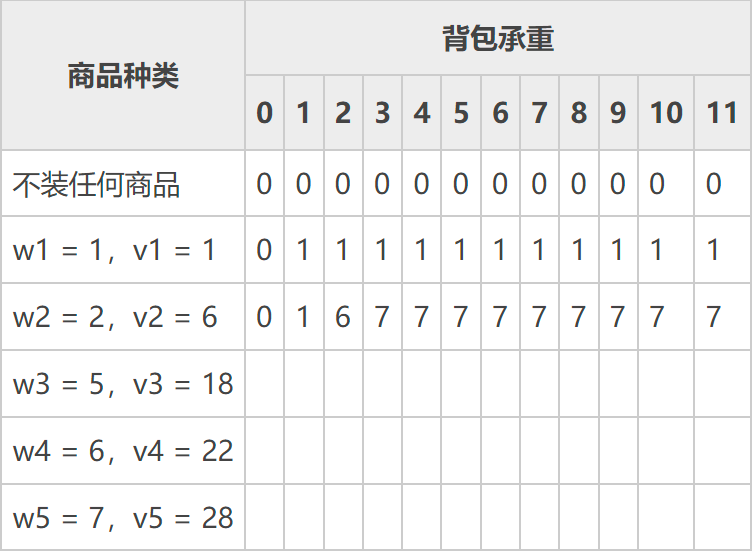
首先考虑将商品一装入各个背包,除了承重值为 0 的背包,其它背包都能装入,且与不装任何商品相比,装入商品一后各个背包的收益更大
我们用 f(n) 表示承重值为 n 的背包对应的最大收益。从算法的角度,各个背包收益值是这样计算的:f(1)=1+f(0)、f(2)=1+f(1)、…、f(11)=1+f(10),其中等号右侧表达式中的 1 指的是商品一的收益值,f(0) - f(10) 指的是不装任何商品时承重分别为 0 - 10 的背包对应的收益值,借助表格可以看到,它们的值都为 0。
-
考虑将商品二装入各个背包,除了承重值为 0 和 1 的背包,其它背包都可以装入。我们可以计算出它们各自对应的收益值:
f(2) = 6 + f(0) = 6
f(3) = 6 + f(1) = 7
f(4) = 6 + f(2) = 7
…
f(9) = 6 + f(7) = 7
f(10) = 6 + f(8) = 7
f(11) = 6 + f(9) = 7等号右侧 f(0)~f(9) 的值是表 2 中装入商品一的各个背包对应的收益值。相比装入商品一统计的各个背包的收益值,装入商品二能使提高各个背包的收益。更新后的表格为:
-
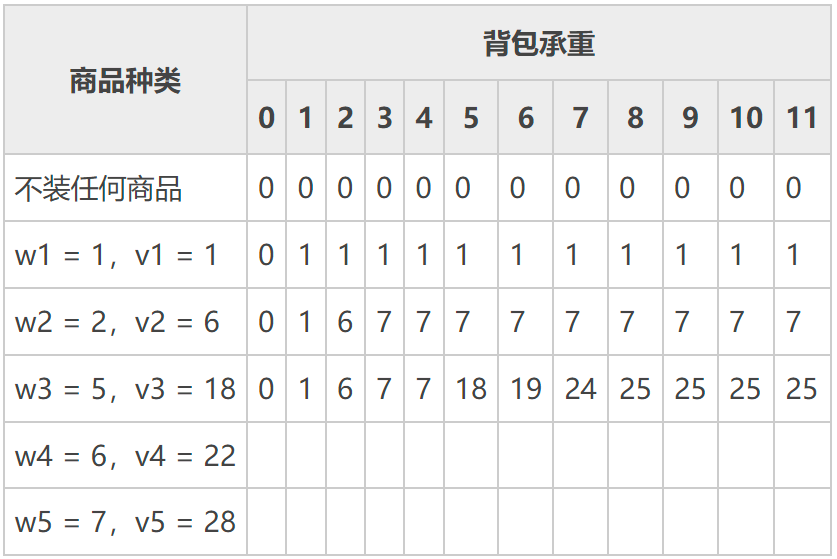
考虑将商品三装入各个背包,除了承重值为小于 5 的背包,其它背包都可以装入。我们可以计算出它们各自对应的收益值:
f(5) = 18 + f(0) = 18
f(6) = 18 + f(1) = 19
f(7) = 18 + f(2) = 24
f(8) = 18 + f(3) = 25
f(9) = 18 + f(4) = 25
f(10) = 18 + f(5) = 25
f(11) = 18 + f(6) = 25等号右侧 f(0)~f(6) 的值是表 2 中装入商品二的各个背包对应的收益值。和装入商品二时统计的各个背包的收益值相比,装入商品三能提高各个背包的收益。更新后的表格为:
-
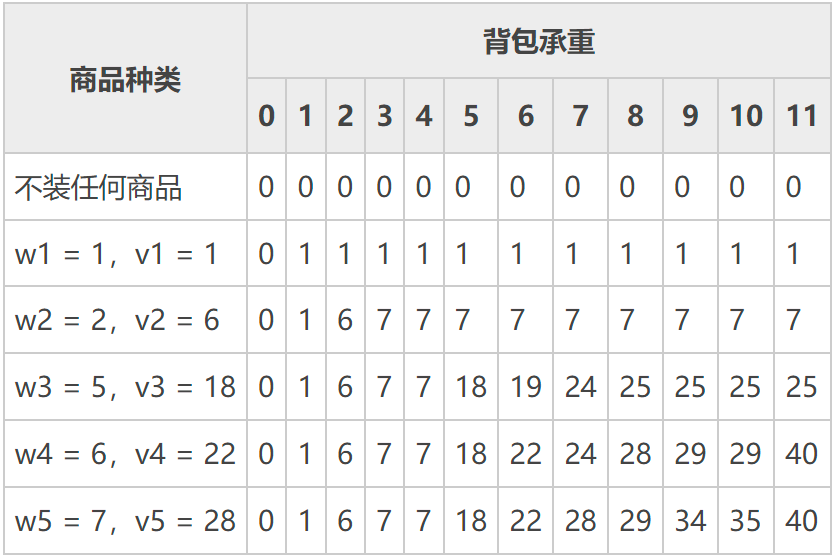
采用同样的方法,我们可以将表 4 中缺失的数据补全,最终得到的表格为:
注意,并不是每试图装入一个新商品,背包的收益一定会提高。举个例子,承重为 7 斤的背包装入商品四时的最大收益是:f(7) = 22+f(1) = 23,装入商品三时最大的收益值为:f(7) = 18+f(2) = 24。因此,上图中承重 7 斤的背包装入商品 4 时对应的收益值仍为 24,并未发生改变。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68internal class Program
{
private static int N = 5; // 商品种类
private static int W = 11; // 背包的最大承重
/*
* 动态规划算法解决01背包问题
* result[N + 1][W + 1]:存储最终的结果
* w[N + 1]:存储各商品的重量
* v[N + 1]:存储各商品的价值
*/
private static void Main(string[] args)
{
int[] w = { 0, 1, 2, 5, 6, 7 };
int[] v = { 0, 1, 6, 18, 22, 28 };
int[,] result = new int[N + 1, W + 1];
knapsack01(result, w, v);
Console.WriteLine("背包承重为 {0},最大收益为 {1}", W, result[N, W]);
Console.Write("选择了:");
select(result, w, v);
}
public static void knapsack01(int[,] result, int[] w, int[] v)
{
// 逐个遍历每个商品
for (int i = 1; i <= N; i++)
{
// 求出从 1 到 W 各个称重对应的最大收益
for (int j = 1; j <= W; j++)
{
// 如果背包载重小于商品总重量,则该商品无法放进背包,收益不变
if (j < w[i])
{
result[i, j] = result[i - 1, j];
}
else
{
// 比较装入该商品和不装该商品,哪种情况获得的收益更大,记录最大收益值
result[i, j] = result[i - 1, j] > (v[i] + result[i - 1, j - w[i]])
? result[i - 1, j] : (v[i] + result[i - 1, j - w[i]]);
}
}
}
}
public static void select(int[,] result, int[] w, int[] v)
{
int n = N;
int bagw = W;
// 逐个商品进行判断
while (n > 0)
{
// 如果在指定载重量下,该商品对应的收益和上一个商品对应的收益相同,则表明未选中
if (result[n, bagw] == result[n - 1, bagw])
{
n--;
}
else
{
// 输出被选用商品的重量和价值
Console.Write($"({w[n]},{v[n]}) ");
bagw = bagw - w[n];
n--;
}
}
}
}